
Imagine the center of a square, then trying to take it's "arc length" as you would a circle, it doesn't work, because a square is a bit different in it's construction and it's properties are different. It does not extend because these arcs don't have circular properties. not a straight line (though equally aplicable if you wished). This arc length problem involves non circular arcs, it is talking about "curve length", i.e. This conversion would give the accurrate answers: 180 degrees * 30 pi / 360 = 15 pi. The arclength in the x-y plane is ALWAYS ( dx² + dy²). This also means we changed the definition for our radians, since 1 degree is now actually equal in length to: Degree = 1/360 * 30pi radians). In our case we changed this value to C = 30 pi. arc length regression & line of best fit surface area and volumes linear.
#ARC LENGTH CALCULUS CALCULATOR FULL#
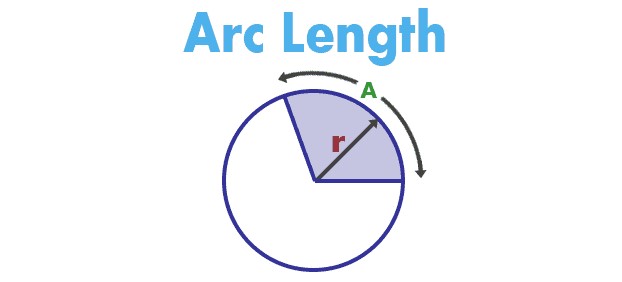
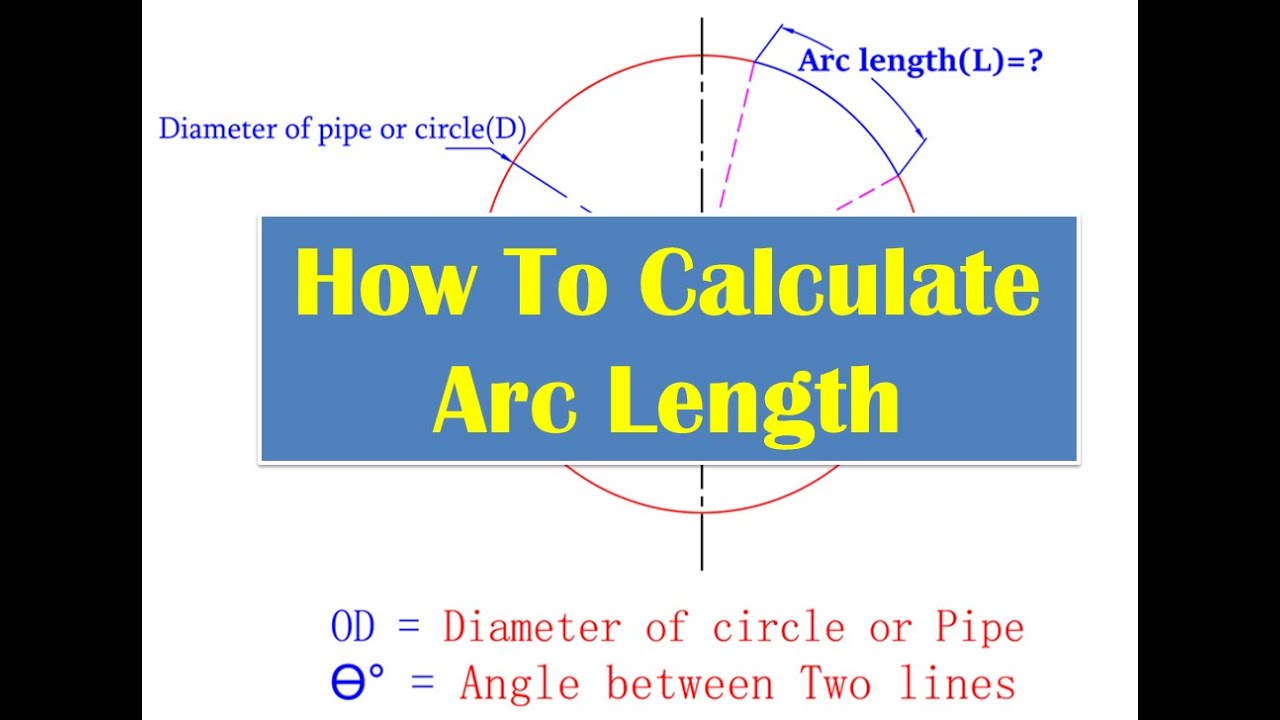
The unit circle is based on a circle with radius of 1, therefore it's diameter it's full circumference is 2pi (it has a diameter of 2, i.e. But our circumference should be 15pi, not just pi. Using our above formula won't simply work: 180 * 2pi / 360 = pi. This logically means an arc with angle measure 180 degrees would have a length of 15pi units (it is half of the circle).

Imagine we had a much larger circle, with diameter 30. This is only for the unit circle however. 45 degrees, and multiplying it by 2pi / 360 to get the radian measure which would be pi/4 radians in this case. We also know that a circle has 2pi radians in it (convertible as 2pi = 360 degrees, thus 1 degree = 2pi / 360 radians) This is where you're getting that, you taking the degree, i.e.
#ARC LENGTH CALCULUS CALCULATOR FREE#
This is because the circumference of a circle is C = pi * d Easily find the arc length of any curve with our free and user-friendly Arc Length Calculator. (This is a stronger condition than having k derivatives, as shown by the second example of Smoothness § Examples.Yes, the arc length you're talking about is changing a circles degree measurement into a measure. If in addition the kth derivative is continuous, then the function is said to be of differentiability class C k. A function that has k successive derivatives is called k times differentiable. Similar examples show that a function can have a kth derivative for each non-negative integer k but not a ( k + 1)th derivative.
DefinitionĪ function of a real variable f( x) is differentiable at a point a of its domain, if its domain contains an open interval I containing a, and the limit L = lim h → 0 f ( a + h ) − f ( a ) h, and it does not have a derivative at zero. Differentiation and integration constitute the two fundamental operations in single-variable calculus. The fundamental theorem of calculus relates antidifferentiation with integration. The reverse process is called antidifferentiation. The process of finding a derivative is called differentiation. For a real-valued function of several variables, the Jacobian matrix reduces to the gradient vector. It can be calculated in terms of the partial derivatives with respect to the independent variables. a closed form formula for the arc length cannot be. StudentCalculus1 ArcLength : find the arc length of a.
Home: Support: Online Help: Education: Student Packages: Calculus 1: Visualization: Arc Length. The Jacobian matrix is the matrix that represents this linear transformation with respect to the basis given by the choice of independent and dependent variables. Maple for Academic Maple for Students Maple Learn Maple Calculator App Maple for Industry and Government Maple. In this generalization, the derivative is reinterpreted as a linear transformation whose graph is (after an appropriate translation) the best linear approximation to the graph of the original function. For this reason, the derivative is often described as the "instantaneous rate of change", the ratio of the instantaneous change in the dependent variable to that of the independent variable.ĭerivatives can be generalized to functions of several real variables. The tangent line is the best linear approximation of the function near that input value. Calculate the area of a sector: A r² × / 2 15² × /4 / 2 88.36 cm². The derivative of a function of a single variable at a chosen input value, when it exists, is the slope of the tangent line to the graph of the function at that point. Calculate the arc length according to the formula above: L r × 15 × /4 11.78 cm. For example, the derivative of the position of a moving object with respect to time is the object's velocity: this measures how quickly the position of the object changes when time advances. Derivatives are a fundamental tool of calculus.

In mathematics, the derivative shows the sensitivity of change of a function's output with respect to the input.


 0 kommentar(er)
0 kommentar(er)
